A fundamental property like causality implies that the optical constants of the material continue in the upper complex plane of photon energies or wavelengths as an analytic function. This is the basis for Kramers-Kronig dispersion relations to obtain ε1 from ε2 or n from k.
This research focuses on such continuation. An interesting property was found: the optical constants get progressively smoother when one enters the upper complex plane and gets farther away from the real axis by increasing the imaginary component of the photon energy, as can be seen in the figure. The continuation to complex energies is found to result in an average of the optical constants with a Lorentzian weight function.
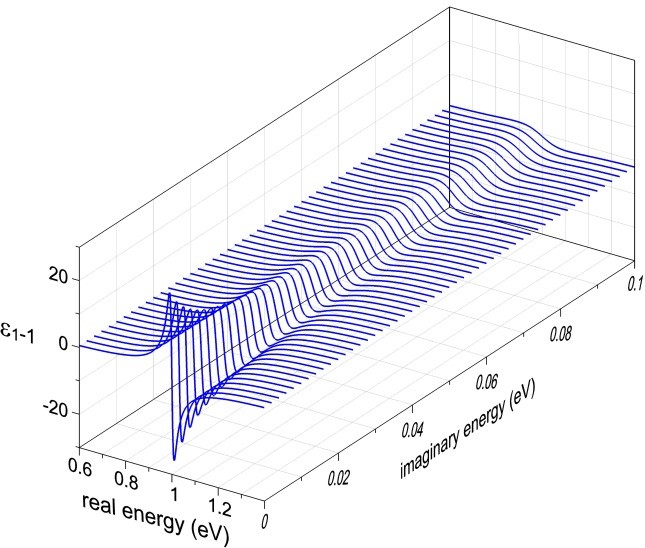
ε1-1 plot for a Lorentz oscillator versus complex photon energy

ε2 plot for a Lorentz oscillator versus complex photon energy
This same optical-constant smoothening is naturally produced in optical constants that have been obtained by means of an optical instrument with a Lorentzian slit function. This smoothening reduces resolution through convolution with the slit function. A procedure that takes advantage of optical constants at complex energies is developed to deconvolve the optical constants. Deconvolution is performed locally, i.e., with no integration, and it consists of shifting the energy of the optical constants by an imaginary amount by means of a Taylor series expansion.
The figure displays the original dielectric function, the effect of convolving it with a Lorentz slit function, and the deconvolution with the present procedure up to second order, which precisely reproduces the original function.

This procedure could be implemented as an analysis tool of a spectrophotometer or an ellipsometer. This tool would enable one to measure optical constants with a modest resolution and to improve it by post-processing them with the present scheme.
Relevant article

